In the example I gave in “Interfacing IPP with Magick++“, I illustrated how to use Intel’s Integrated Performance Primitives (IPP) to perform edge detection. One issue with Canny edge detection algorithm is that we need to specify a high threshold and a low threshold. How to select those threshold values affect the quality of the detected edge greatly. And in my previous example, the threshold values were chosen manually. In this blog post, I will examine a couple of simple methods that can be used to automatically determine the threshold values.

The simplest way is to use the mean value of the gray scale image pixel values. As a rule of thumb, we set the low threshold to 0.66*[mean value] and set the high threshold to 1.33*[mean value]. Another way is to use the median color in the gray scale image and uses 0.66*[median value] and 1.33*[median value] accordingly. For typical images, these two methods achieve comparable results.

For example, the following shows the picture of a building along with its histogram (original image from Microsoft Research Digital Image. Please see Microsoft Research Digital Image License Agreement for more information):

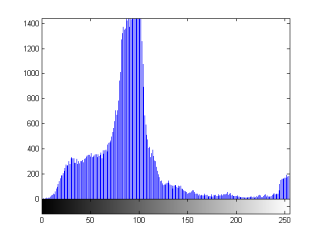The following shows the edge detection results using Canny algorithm (left image uses mean value auto-thresholding, right image uses median value auto-thresholding) and the results exhibit very little visible differences.

However, for images has non-equalized histogram (see the picture of cloud and its histogram below):

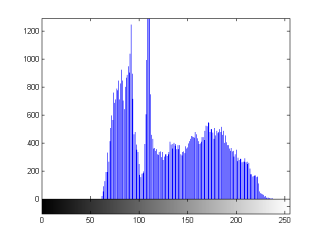Canny Edge detection result based on mean value auto-thresholding is pretty poor (see image on the left below), while edge detection based on median value auto-thresholding achieved much better result (see image on the right below)

Alternatively, we could have performed histogram equalization on the image first before applying Canny edge detection with mean auto-thresholding:

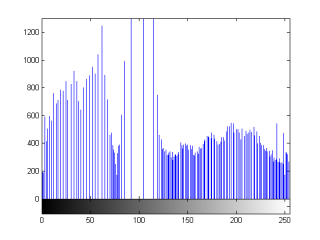And after image equalization, both mean and median value auto-thresholding achieved similar results.

So the Canny edge detection using median value auto-thresholding seems to adapt to different types of images very well (note selecting the median value selection can be thought as equalizing the histogram, except that the pixel values are not changed during such operation).

The following is the code listing for the histogram calculation using IPP (based on the image class I created earlier)

/** @brief Get the min max mean value statistics for the current image
 *   @param min, max, mean: these are output parameters that are passed
 *         back by reference.
 */
void IPPGrayImage::MinMaxMean(float& min, float& max, double& mean)
{
    IppStatus sts;
    IppiSize origImgSize = {_width, _height};

    sts = ippiMinMax_32f_C1R(_imgBuffer, _width * PIXEL_SIZE, origImgSize, &min, &max);
    assert(sts == ippStsNoErr);
    sts = ippiMean_32f_C1R(_imgBuffer, _width * PIXEL_SIZE, origImgSize, &mean, ippAlgHintFast);
    assert(sts == ippStsNoErr);
}

/** @brief Calculate the histogram of the image
 *   @param nLevel: the number of bins in the histogram
 *        levels: this is the optional levels user can pass in (histogram will be then
 *                calculated with these levels instead of the uniform levels by default.
 *   @return an integer array which contains the histogram.
 *   @note the histogram is by default calculated using uniform bins across the color range.
 */
unsigned int * IPPGrayImage::GetHistogram(unsigned int nLevel, float levels[])
{
    IppStatus sts;
    Ipp32f* l = new Ipp32f[nLevel];
    IppiSize origImgSize = {_width, _height};

    unsigned int* bins = new unsigned int[nLevel - 1];

    float minVal = 0, maxVal = 0, stepVal = 0;
    double meanVal = 0;
    if (levels != NULL)
    {
        for (unsigned int i = 0; i < nLevel; i++)
        {
            l[i] = levels[i];
        }
    }
    else
    {
        MinMaxMean(minVal, maxVal, meanVal);
        stepVal = (maxVal - minVal) / (float) nLevel;

        for (unsigned int i = 0; i < nLevel; i++)
        {
            l[i] = minVal + stepVal * i;
        }
    }

    sts = ippiHistogramRange_32f_C1R(_imgBuffer, _width * PIXEL_SIZE, origImgSize, (Ipp32s*) bins, (Ipp32f*) l, nLevel);
    return bins;
}

Be Sociable, Share!

•